관성 모멘트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

관성 모멘트는 회전하는 물체의 관성을 나타내는 물리량으로, 물체의 질량과 회전축으로부터의 거리에 따라 결정된다. 스칼라, 텐서 형태로 표현되며, 각운동량, 각속도, 토크, 각가속도 등과 밀접한 관련이 있다. 물체의 질량중심을 지나는 축에 대한 관성 모멘트는 최소값을 가지며, 평행축 정리를 통해 다른 축에 대한 관성 모멘트를 계산할 수 있다. 관성 모멘트는 물체의 회전 운동 에너지, 플라이휠 효과 등과 관련 있으며, 공학 분야에서 회전체의 에너지 저장 및 제어에 활용된다.

더 읽어볼만한 페이지

강체 - 자유도 (역학)
자유도는 물리학에서 계의 상태를 나타내는 독립 변수의 최소 개수를 의미하며, 강체의 경우 병진 및 회전 운동을 포함하여 최대 6개의 자유도를 갖고, 이는 메커니즘 설계 및 분석에 중요한 역할을 하며 로봇 공학 등 다양한 분야에 응용된다.
강체 - 오일러 운동 방정식
오일러 운동 방정식은 한 점이 고정된 강체에 작용하는 돌림힘과 강체의 각운동량, 각속도, 관성 모멘트 간의 관계를 나타내는 세 개의 미분 방정식이다.
모멘트 (물리학) - 각운동량
각운동량은 회전 운동량을 나타내는 물리량으로, 질점의 경우 위치 벡터와 선운동량의 벡터곱으로 정의되며, 외부 토크가 없을 때 보존되고, 양자역학에서는 양자화되는 특성을 지닌다.
모멘트 (물리학) - 운동량
운동량은 물체의 질량과 속도의 곱으로 정의되는 벡터량으로, 외부 힘이 작용하지 않는 계에서는 보존되며, 충돌, 충격량, 질량 변화, 상대론, 해석역학, 전자기학, 양자역학 등 다양한 역학 분야에서 중요한 물리량으로 다뤄진다.
역학 - 운동량
운동량은 물체의 질량과 속도의 곱으로 정의되는 벡터량으로, 외부 힘이 작용하지 않는 계에서는 보존되며, 충돌, 충격량, 질량 변화, 상대론, 해석역학, 전자기학, 양자역학 등 다양한 역학 분야에서 중요한 물리량으로 다뤄진다.
역학 - 역학 (물리학)
역학은 물체의 운동과 힘의 상호작용을 연구하는 물리학의 한 분야로, 고대부터 뉴턴의 고전 역학 정립, 그리고 아인슈타인의 상대성이론과 양자역학을 거쳐 현대 역학으로 발전해 왔으며, 다양한 하위 분야와 공학 분야에 응용되고 뉴턴의 운동 법칙을 기본 원리로 한다.

관성 모멘트

2. 정의

관성 모멘트는 물체가 회전 운동의 변화에 저항하는 정도를 나타내는 물리량이다. 쉽게 말해, 물체가 얼마나 회전하기 어려운지를 나타낸다. 예를 들어, 질량이 같지만 반지름이 다른 두 원판을 비교했을 때, 반지름이 큰 원판은 같은 각속도로 회전할 때 바깥쪽이 더 빠르게 움직여야 하므로 회전시키기 더 어렵다. 따라서 반지름이 큰 원판의 관성 모멘트가 더 크다.

관성 모멘트는 크게 두 가지 형태로 나타낼 수 있다. 하나는 스칼라 형태로, 회전축이 고정된 간단한 경우에 사용된다. 예를 들어, 도르래와 같이 회전축이 고정된 물체의 운동은 스칼라 관성 모멘트를 사용하여 간단하게 설명할 수 있다.

다른 하나는 텐서 형태로, 회전축이 변하는 복잡한 운동을 다룰 때 사용된다. 각운동량 벡터와 각속도 벡터가 평행하지 않은 경우, 스칼라 형태로는 이 둘 사이의 관계를 정확하게 나타낼 수 없기 때문이다. 자이로스코프, 팽이, 인공위성의 운동 등이 텐서 형태의 관성 모멘트를 사용해야 하는 대표적인 예시이다.

기계공학에서는 단면 이차 모멘트와 구별하기 위해 관성 모멘트를 '질량 관성 모멘트'라고 부르기도 한다. 또한, 관성 모멘트는 물체가 비틀림에 저항하는 정도를 나타내는 극관성모멘트와 혼동하지 않도록 주의해야 한다.

피겨 스케이팅 선수가 회전할 때 팔을 안으로 당겨 관성 모멘트를 줄이면 각운동량 보존에 따라 더 빨리 회전할 수 있다.

회전 의자 실험 영상. 관성 모멘트를 보여준다. 회전하는 교수가 팔을 당기면 관성 모멘트가 감소하고, 각운동량을 보존하기 위해 각속도가 증가한다.

어떤 주어진 축을 중심으로 회전하는 점질량의 스칼라 관성 모멘트는 다음과 같이 정의된다.

:

I = m r^2

여기서

$m$ 은 질량
$r$ 은 회전축으로부터 점질량까지의 거리

이다.

같은 축을 중심으로 회전하는 여러 점질량들의 총 관성 모멘트는 각 점질량들의 관성 모멘트를 모두 더한 값과 같다.

:

I = \sum_{i=1}^n m_i r_i^2

만약 질량이 공간에 연속적으로 분포되어 있다면, 적분을 사용하여 스칼라 관성 모멘트를 다음과 같이 정의할 수 있다.

:

I = \int r^2\,dm = \int_V r^2 \rho(\mathbf{r}) \, dV

물체가 축 주위로 자유롭게 회전할 때, 토크를 가해야 각운동량을 변화시킬 수 있다. 주어진 각가속도(각속도의 변화율)를 발생시키는 데 필요한 토크의 양은 물체의 관성 모멘트에 비례한다.

관성 모멘트는 회전 운동에서 질량이 직선 운동에서 하는 역할과 비슷하다. 둘 다 물체의 운동 변화에 대한 저항을 나타낸다. 관성 모멘트는 회전축 주위에 질량이 어떻게 분포되어 있는지에 따라 달라지며, 선택한 축에 따라 값이 달라진다.

1673년 크리스티안 하위헌스는 복합진자 연구에서 이 개념을 도입했고,^[2] 레온하르트 오일러가 1765년 "관성 모멘트"라는 용어를 처음 사용했다.^[2]^[3]

2. 1. 스칼라 관성 모멘트

관성 모멘트는 물체가 주어진 축을 중심으로 회전 운동을 유지하려는 경향을 나타내는 물리량이다. 질량이 같더라도 반지름이 큰 물체일수록 회전시키기 어렵다. 예를 들어, 반지름이 큰 원판 A는 반지름이 작은 원판 B보다 같은 각속도로 회전할 때 바깥쪽이 더 빠르게 움직여야 하므로, A를 회전시키는 것이 B를 회전시키는 것보다 어렵다. 이러한 특성을 설명하는 물리량이 관성 모멘트이며, 이 경우 A의 관성 모멘트가 B보다 크다.

스칼라 형태의 관성 모멘트는 주로 회전축이 고정된 간단한 경우에 사용된다. 예를 들어, 도르래와 같이 회전축이 고정된 물체는 스칼라 형태를 사용하여 물리량 사이의 관계를 간단하게 나타낼 수 있다.

차원 분석을 통해 관성 모멘트의 식을 간단히 유추하면 다음과 같다.

:

I = k \cdot m \cdot {r}^2 \,\!

여기서,

$m$ : 질량
$r$ : 질량중심으로부터 회전축까지의 거리 또는 물체의 반지름과 같은 물체를 특정짓는 길이.
$k$ : '''관성 상수'''(inertia constant^영어). 물체의 모양에 따라 값이 바뀐다.

관성 상수는 물체 내부의 질량 배치에 따라 달라지는 값이다. 몇 가지 예는 다음과 같다.

$k=1$ : 두께가 매우 얇은 원통, $r$ 은 원통의 반지름
$\textstyle k=\frac{2}{5}$ : 꽉 찬 구, $r$ 은 구의 반지름
$\textstyle k=\frac{1}{2}$ : 속이 꽉 찬 원통 또는 원판, $r$ 은 원통 또는 원판의 반지름

관성 상수의 값들은 관성 모멘트의 목록에 수록되어 있다.

관성 모멘트 I는 또한 계의 총 각운동량 L을 주축 주위의 각속도 ω로 나눈 값으로 정의된다.^[8]^[9] 즉,

:

I = \frac{L}{\omega}.

계의 각운동량이 일정하다면 관성 모멘트가 작아질수록 각속도는 증가해야 한다. 이는 회전하는 피겨 스케이터가 뻗은 팔을 안으로 당기거나 다이버가 다이빙 중에 몸을 웅크리는 자세로 만들어 더 빨리 회전할 때 발생한다.^[8]^[9]^[10]^[11]^[12]^[13]^[14]

물체의 모양이 변하지 않으면 관성 모멘트는 뉴턴 운동 법칙에 물체에 작용하는 토크 τ와 주축 주위의 각가속도 α의 비율로 나타난다. 즉,

:

\tau = I \alpha.

단진자의 경우 이 정의는 진자의 질량 m과 회전축으로부터의 거리 r에 대한 관성 모멘트 I에 대한 공식을 다음과 같이 제공한다.

:

I = mr^2.

따라서 진자의 관성 모멘트는 물체의 질량 m과 회전축까지의 거리 r로 정의된 기하학적 형태 모두에 따라 달라진다.

이 간단한 공식은 임의의 형태를 가진 물체에 대해 관성 모멘트를 각 요소 점 질량 dm을 축 k에 대한 수직 거리 r의 제곱으로 곱한 값들의 합으로 정의하는 것으로 일반화된다. 따라서 임의의 물체의 관성 모멘트는 질량의 공간 분포에 따라 달라진다.

일반적으로 질량 m을 가진 물체가 주어지면 특정 회전축에 따라 의존하는 유효 반지름 k를 정의할 수 있으며, 이 반지름을 사용하면 축 주위의 관성 모멘트는 다음과 같다.

:

I = m k^2,

여기서 k는 축 주위의 회전반경으로 알려져 있다.

수학적으로 단순진자의 관성 모멘트는 진자의 회전축에 대한 중력에 의한 토크와 그 회전축에 대한 각가속도의 비율이다. 단순진자의 경우 이는 질점의 질량 m과 회전축까지의 거리 r의 제곱의 곱으로 나타낼 수 있다. 즉,

:

I = mr^2.

이는 다음과 같이 보일 수 있다. 단순진자의 질량에 작용하는 중력은 진자 운동면에 수직인 축 주위에 토크

\boldsymbol{\tau} = \mathbf{r} \times \mathbf{F}

를 발생시킨다. 여기서

\mathbf{r}

은 토크 축에서 진자 질량중심까지의 거리 벡터이고,

\mathbf{F}

는 질량에 작용하는 알짜힘이다. 이 토크에는 이 축 주위의 끈과 질량의 각가속도

\boldsymbol{\alpha}

가 관련되어 있다. 질량이 원에 구속되어 있으므로 질량의 접선 가속도는

\mathbf{a} = \boldsymbol{\alpha} \times \mathbf{r}

이다.

\mathbf F = m \mathbf a

이므로 토크 방정식은 다음과 같다.

:

\begin{align}\boldsymbol{\tau}&= \mathbf{r} \times \mathbf{F}= \mathbf{r} \times (m \boldsymbol{\alpha} \times \mathbf{r}) \\&= m \left(\left(\mathbf{r} \cdot \mathbf{r}\right) \boldsymbol{\alpha} - \left(\mathbf{r} \cdot \boldsymbol{\alpha}\right) \mathbf{r}\right) \\&= mr^2 \boldsymbol{\alpha}= I\alpha \mathbf{\hat{k}},\end{align}

여기서

\mathbf{\hat{k}}

는 진자의 면에 수직인 단위 벡터이다. (마지막에서 두 번째 단계는

\boldsymbol{\alpha}

와

\mathbf{r}

의 수직성을 이용한 벡터 삼중곱 전개를 사용한다.)

I = mr^2

는 이 단일 질량의 회전축에 대한 ''관성 모멘트''이다.

I = mr^2

는 단순진자의 각운동량에도 나타나는데, 이는 회전축 주위의 진자 질량의 속도

\mathbf{v} = \boldsymbol{\omega} \times \mathbf{r}

로부터 계산되며, 여기서

\boldsymbol{\omega}

는 회전축에 대한 질량의 각속도이다. 이 각운동량은 다음과 같이 주어집니다.

:

\begin{align}\mathbf{L}&= \mathbf{r} \times \mathbf{p}= \mathbf{r} \times \left(m\boldsymbol{\omega} \times \mathbf{r}\right) \\& = m\left(\left(\mathbf{r} \cdot \mathbf{r}\right)\boldsymbol{\omega} - \left(\mathbf{r} \cdot \boldsymbol{\omega}\right)\mathbf{r}\right) \\&= mr^2 \boldsymbol{\omega}= I\omega\mathbf{\hat{k}},\end{align}

이전 방정식과 유사한 유도를 사용한다.

마찬가지로 진자 질량의 운동 에너지는 회전축 주위의 진자 속도로 정의되어

:

E_\text{K} = \frac{1}{2} m \mathbf{v} \cdot \mathbf{v} = \frac{1}{2} \left(mr^2\right)\omega^2 = \frac{1}{2}I\omega^2.

이것은

I = mr^2

이 질량이 어떻게 물체의 형태와 결합하여 회전 관성을 정의하는지를 보여준다. 임의의 모양을 가진 물체의 관성 모멘트는 물체의 모든 질량 요소에 대한

mr^2

값의 합이다.

1897년 과학 저널에 실린 멘덴홀 중력계 장치에 사용된 진자들. 토마스 C. 멘덴홀이 1890년에 개발한 휴대용 중력계는 지구의 국지적 중력장에 대한 가장 정확한 상대 측정값을 제공했다.

복합진자는 회전축 주위를 강체로 회전하는 연속적인 형태의 입자들의 집합체로 이루어진 물체이다. 복합진자의 관성 모멘트는 그것을 구성하는 각 입자의 관성 모멘트의 합이다.^[15]^[16]^[17] 복합진자의 고유 진동수 (

\omega_\text{n}

)는 관성 모멘트

I_P

에 따라 달라지며,

:

\omega_\text{n} = \sqrt{\frac{mgr}{I_P}},

로 나타낼 수 있다. 여기서

m

은 물체의 질량,

g

는 국지적 중력 가속도,

r

은 회전축에서 물체의 질량 중심까지의 거리이다. 작은 각변위에 대한 이 진동 주파수를 측정하면 물체의 관성 모멘트를 효과적으로 측정할 수 있다.^[22]

따라서 물체의 관성 모멘트를 결정하려면, 편리한 회전축

P

에 물체를 매달아 원하는 관성 모멘트 방향에 수직인 평면에서 자유롭게 진동하도록 한 다음, 고유 진동수 또는 진동 주기 (

t

)를 측정하여 다음 식을 얻는다.

:

I_P = \frac{mgr}{\omega_\text{n}^2} = \frac{mgrt^2}{4\pi^2},

여기서

t

는 진동 주기(지속 시간)이며, 일반적으로 여러 주기의 평균값을 사용한다.

미끄러짐 없이 평면을 따라 경주하는 동일한 질량과 반지름을 가진 네 개의 물체. 뒤에서부터 앞으로: 도착선에 도달하는 시간은 관성 모멘트가 더 큰 물체일수록 더 길다.

물체의 축에 대한 관성 모멘트는 물체의 모든 입자에 대해

mr^2

을 합산하여 계산한다. 여기서

r

은 지정된 축에 대한 수직 거리이다. 확장된 물체의 운동 연구에서 관성 모멘트가 어떻게 발생하는지 확인하려면 강체 점 질량 조립체를 고려하는 것이 편리하다. (이 방정식은 이것이 관성 모멘트를 완전히 설명하지 않는다는 것을 이해한다면 주축이 아닌 축에도 사용할 수 있다.^[21])

N

개의 질량

m_i

가 회전축의 가장 가까운 점인 피벗 지점

P

에서

r_i

거리에 있는 조립체의 운동 에너지를 고려해 보자. 이것은 개별 질량의 운동 에너지의 합이다.^[22]^[23]

:

E_\text{K} =\sum_{i=1}^N \frac{1}{2}\,m_i \mathbf{v}_i \cdot \mathbf{v}_i =\sum_{i=1}^N \frac{1}{2}\,m_i \left(\omega r_i\right)^2 =\frac12\, \omega^2 \sum_{i=1}^N m_i r_i^2.

이것은 물체의 관성 모멘트가 각

mr^2

항의 합임을 보여준다. 즉,

:

I_P = \sum_{i=1}^N m_i r_i^2.

따라서 관성 모멘트는 회전축 주위의 입자의 질량과 분포를 결합하는 물리적 특성이다. 동일한 물체의 서로 다른 축을 중심으로 한 회전은 서로 다른 관성 모멘트를 생성한다.

지정된 축을 중심으로 회전하는 연속체의 관성 모멘트는 무한히 많은 점 입자를 제외하고는 동일한 방식으로 계산된다. 따라서 합산의 한계가 제거되고 합은 다음과 같이 작성된다.

:

I_P = \sum_i m_i r_i^2

다른 표현식은 합

2. 2. 관성 텐서

텐서에는 두 종류가 있다. 도르래와 같이 회전축이 고정되어 있는 물체는 스칼라 형태를 사용하면 간단히 물리량 사이의 관계를 기술할 수 있다. 하지만, 회전축이 변하는 운동과 같은 복잡한 경우엔 각운동량 벡터와 각속도 벡터가 평행하지 않아 스칼라로 이 둘 사이의 관계를 기술하는게 불충분하기 때문에 텐서 형태를 사용한다. 이러한 경우의 예로 자이로스코프, 팽이, 인공위성의 운동이 있다.^[6]^[7]

일반적으로 물체가 모든 축에 대해 대칭이 아닌 한 관성 모멘트는 같지 않다. '''관성 텐서'''는 하나의 양으로 물체의 모든 관성 모멘트를 요약하는 편리한 방법이다. 이는 공간의 어떤 점에 대해서도 계산될 수 있지만, 실제로는 질량 중심이 가장 일반적으로 사용된다.

관성 텐서

\mathbf{I}

는 계수가 2인 대칭 텐서, 즉, 2차 대칭 텐서로 점질량

m_k

들로 구성된 강체의 경우 관성 텐서의 데카르트 좌표계에서의 성분은 다음과 같이 정의한다.

:

\mathbf{I} = \begin{bmatrix}I_{xx} & I_{xy} & I_{xz} \\I_{yx} & I_{yy} & I_{yz} \\I_{zx} & I_{zy} & I_{zz}\end{bmatrix}

:

I_{ij} \ \stackrel{\mathrm{def}}{=}\  \sum_k m_{k} (r_k^{2}\delta_{ij} - r_{ki}r_{kj})\,\!

여기서

$i$ , $j$ : x, y, 또는 z좌표를 나타내는 지표, 순서대로 1, 2, 3에 대응된다.
$\mathbf{r}_k$ : 어떤 기준점으로부터 $k$ 번째 점질량까지의 방향 벡터.
$\delta_{ij}$ : 크로네커 델타

이다. 대각항은 아래와 같이 간단히 쓸 수도 있다.

:

I_{xx} \ \stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k} (y_{k}^{2}+z_{k}^{2})

:

I_{yy} \ \stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k} (x_{k}^{2}+z_{k}^{2})

:

I_{zz} \ \stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k} (x_{k}^{2}+y_{k}^{2})

'''관성의 곱'''(products of inertia^영어)이라 불리기도 하는 비대각항들은 아래와 같이 쓰기도 한다.

:

I_{xy} = I_{yx} \ \stackrel{\mathrm{def}}{=}\  -\sum_{k=1}^{N} m_{k} x_{k} y_{k}

:

I_{xz} = I_{zx} \ \stackrel{\mathrm{def}}{=}\  -\sum_{k=1}^{N} m_{k} x_{k} z_{k}

:

I_{yz} = I_{zy} \ \stackrel{\mathrm{def}}{=}\ -\sum_{k=1}^{N} m_{k} y_{k} z_{k}

여기서

I_{xx}

는 x축을 기준으로 하며 x축을 중심으로 회전하는 경우의 관성 모멘트,

I_{xy}

는 y축을 기준으로 하며 x축을 중심으로 회전하는 경우의 관성 모멘트 등을 말한다.

N개의 점 질량 m_k를 갖는 강체의 경우, 관성 모멘트 텐서는 다음과 같이 주어진다.

\mathbf{I} = \begin{bmatrix}I_{11} & I_{12} & I_{13} \\I_{21} & I_{22} & I_{23} \\I_{31} & I_{32} & I_{33}\end{bmatrix}.

그 성분은 다음과 같이 정의된다.

I_{ij} \ \stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k}\left(\left\|\mathbf{r}_k\right\|^{2}\delta_{ij} - x_{i}^{(k)}x_{j}^{(k)}\right)

여기서,

i, j는 각각 x, y, z에 대해 1, 2 또는 3과 같고,
r_k = (x₁^(k), x₂^(k), x₃^(k))는 텐서가 계산되는 점으로부터 점 질량 m_k까지의 벡터이고,
δ_ij는 크로네커 델타이다.

정의에 따라 I는 대칭 텐서이다.

대각선 요소는 다음과 같이 간결하게 쓸 수 있다.

\begin{align}I_{xx} \ &\stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k} \left(y_{k}^{2} + z_{k}^{2}\right), \\I_{yy} \ &\stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k} \left(x_{k}^{2} + z_{k}^{2}\right), \\I_{zz} \ &\stackrel{\mathrm{def}}{=}\  \sum_{k=1}^{N} m_{k} \left(x_{k}^{2} + y_{k}^{2}\right),\end{align}

비대각선 요소는 '''관성곱'''이라고도 하며 다음과 같다.

\begin{align}I_{xy} = I_{yx} \ &\stackrel{\mathrm{def}}{=}\  -\sum_{k=1}^{N} m_{k} x_{k} y_{k}, \\I_{xz} = I_{zx} \ &\stackrel{\mathrm{def}}{=}\  -\sum_{k=1}^{N} m_{k} x_{k} z_{k}, \\I_{yz} = I_{zy} \ &\stackrel{\mathrm{def}}{=}\  -\sum_{k=1}^{N} m_{k} y_{k} z_{k}.\end{align}

여기서 I_xx는 물체가 x축을 중심으로 회전할 때 x축 주위의 관성 모멘트를 나타내고, I_xy는 물체가 x축을 중심으로 회전할 때 y축 주위의 관성 모멘트를 나타내는 등이다.

이러한 값들은 질량 밀도 함수로 설명되는 분포된 질량을 가진 물체로 스칼라 관성 모멘트와 유사한 방식으로 일반화할 수 있다. 그러면 다음을 얻는다.

\mathbf{I} = \iiint_V \rho(x,y,z) \left( \|\mathbf{r}\|^2 \mathbf{E}_{3} - \mathbf{r}\otimes \mathbf{r}\right)\, dx \, dy \, dz,

여기서 r⊗r은 외적이고, E₃는 3×3 단위 행렬이며, V는 물체를 완전히 포함하는 공간 영역이다.

또는 각운동량 연산자 [r]x = r×x의 관점에서도 쓸 수 있다.

\mathbf{I} = \iiint_V \rho(\mathbf{r}) [\mathbf r]^\textsf{T}[\mathbf r] \, dV = -\iiint_{Q} \rho(\mathbf{r}) [\mathbf r]^2 \, dV

관성 텐서는 관성 행렬과 같은 방식으로 n 방향의 임의의 축에 대한 스칼라 관성 모멘트를 계산하는 데 사용할 수 있다.

I_n = \mathbf{n}\cdot\mathbf{I}\cdot\mathbf{n},

여기서 점곱은 구성 요소 텐서의 해당 요소와 함께 수행된다. I₁₂와 같은 관성곱 항은 다음 계산으로 얻을 수 있다.

I_{12} = \mathbf{e}_1\cdot\mathbf{I}\cdot\mathbf{e}_2,

그리고 물체가 y축 주위로 회전할 때 x축 주위의 관성 모멘트로 해석될 수 있다.

2차 텐서의 성분은 행렬로 조립할 수 있다. 관성 텐서의 경우 이 행렬은 다음과 같이 주어진다.

\mathbf{I} = \begin{bmatrix}I_{11} & I_{12} & I_{13} \\[1.8ex]I_{21} & I_{22} & I_{23} \\[1.8ex]I_{31} & I_{32} & I_{33}\end{bmatrix} = \begin{bmatrix}I_{xx} & I_{xy} & I_{xz} \\[1.8ex]I_{yx} & I_{yy} & I_{yz} \\[1.8ex]I_{zx} & I_{zy} & I_{zz}\end{bmatrix} = \begin{bmatrix}\sum_{k=1}^{N} m_{k} \left(y_{k}^2 + z_{k}^2\right) &

\sum_{k=1}^{N} m_{k} x_{k} y_{k} &
\sum_{k=1}^{N} m_{k} x_{k} z_{k} \\[1ex]
\sum_{k=1}^{N} m_{k} x_{k} y_{k} &

\sum_{k=1}^{N} m_{k} \left(x_{k}^2 + z_{k}^2\right) &

\sum_{k=1}^{N} m_{k} y_{k} z_{k} \\[1ex]
\sum_{k=1}^{N} m_{k} x_{k} z_{k} &
\sum_{k=1}^{N} m_{k} y_{k} z_{k} &

\sum_{k=1}^{N} m_{k} \left(x_{k}^2 + y_{k}^2\right)\end{bmatrix}.

강체 역학에서는 I_xx 및 I_xy와 같이 관성 텐서의 성분에 대해 x축, y축 및 z축을 명시적으로 식별하는 표기법을 사용하는 것이 일반적이다.

질점계가 어떤 회전축 주위를 일정한 각속도 벡터로 회전할 때, 질점계가 가지는 각운동량 벡터는 다음과 같이 표현할 수 있다.

:

여기서는 번째 질점의 질량, 는 회전축 상의 원점과의 상대 좌표이며 는 그 크기이다. 이 식에서 알 수 있듯이, 은 와 방향이 반드시 일치하지 않지만, 의 선형 변환으로 나타낼 수 있다. 즉, 그 선형 변환을 라 하면,

:

으로 표현할 수 있다. 이 변환 는 2계 텐서이며, 과 의 각 성분은

:

\begin{align}L_{j} &= \sum_{k = 1}^3 I_{j k} \omega_k \\I_{j k} &= \sum_i m_i \left( r_i^2 \delta_{j k} - r_{i, j} r_{i, k} \right)\end{align}

과 같은 형태로 표현된다. 여기서 는 크로네커 델타, 는 벡터 의 성분이다. 를 행렬로 표시하면

:

이 된다. 이 정의로부터 는 대칭 텐서이다. 이 2계 텐서 를 '''관성 모멘트 텐서''' 또는 간단히 '''관성 텐서'''라고 부른다. 또한, 관성 텐서의 대각 성분 ，，를 (각각 ，， 축에 대한) '''관성 모멘트 계수''' ()라고 부르며, ，，는 '''관성곱''' ()라고 부른다.

참고로, 질량 분포가 연속적으로 퍼져 있는 경우에는, 그 물체의 관성 텐서는 밀도를 사용하여

:

이 된다.

3. 성질

일반적으로 강체의 관성 모멘트는 강체의 질량에 비례하며, 질량이 회전축으로부터 멀리 분포할수록 커진다.

회전축이 질량 중심을 지날 때 관성 모멘트는 최솟값을 가지며, 축이 질량 중심으로부터 멀리 떨어져 있을 경우, 그 축 주위의 관성 모멘트는 평행축 정리를 통해 쉽게 구할 수 있다.^[38]

각속도로 회전하는 물체의 회전 운동 에너지는 관성 텐서와 각속도의 곱으로 나타낼 수 있으며,^[39] 토크는 각운동량을 바꾸는데 필요하며, 물체의 관성 모멘트에 비례한다. 이처럼 관성 모멘트는 회전 운동에서 질량과 같이 물체의 운동 변화에 대한 저항을 나타낸다.

1920년대 존디어 트랙터의 엔진에 있는 바퀴살이 있는 플라이휠. 플라이휠의 큰 관성 모멘트는 트랙터의 작동을 부드럽게 한다.

3. 1. 평행축 정리

어떤 물체의 질량 중심을 지나는 회전축에 대한 관성 모멘트를 구하면, 그와 평행한 다른 회전축을 기준으로 회전하는 물체의 관성 모멘트는 복잡한 계산 없이 간단하게 구할 수 있다. 이 관계를 평행축 정리라고 한다.^[4]^[7]

:

I = I_{\textrm{cm}} + md^2

여기서,

$\textstyle I_{\textrm{cm}}$ : 질량 중심을 지나는 회전축에 대한 관성 모멘트
$m$ : 물체의 질량
$d$ : 두 회전축 사이의 거리

이다.

강체의 관성 모멘트는 기준점의 선택에 따라 달라진다. 질량중심

\mathbf{C}

를 기준으로 한 관성 모멘트와 다른 점

\mathbf{R}

를 기준으로 한 관성 모멘트 사이에는 유용한 관계가 있는데, 이를 평행축 정리라고 한다.

기준점

\mathbf{R}

를 기준으로 측정한 강체 입자계의 관성 모멘트 행렬

\mathbf{I_R}

는 다음과 같이 주어진다.

:

\mathbf{I}_\mathbf{R} = -\sum_{i=1}^n m_i\left[\mathbf{r}_i - \mathbf{R}\right]^2.

\mathbf{C}

를 강체계의 질량중심이라고 하면,

:

\mathbf{R} = (\mathbf{R} - \mathbf{C}) + \mathbf{C} = \mathbf{d} + \mathbf{C},

여기서

\mathbf{d}

는 질량중심

\mathbf{C}

에서 기준점

\mathbf{R}

로 향하는 벡터이다. 이 식을 사용하여 관성 모멘트 행렬을 계산하면,

:

\mathbf{I}_\mathbf{R}= -\sum_{i=1}^n m_i[\mathbf{r}_i - \left(\mathbf{C} + \mathbf{d}\right)]^2= -\sum_{i=1}^n m_i[\left(\mathbf{r}_i - \mathbf{C}\right) - \mathbf{d}]^2.

외적에 대해 분배하면 다음을 얻는다.

:

\mathbf{I}_\mathbf{R} =

\left(\sum_{i=1}^n m_i [\mathbf{r}_i - \mathbf{C}]^2\right)

+ \left(\sum_{i=1}^n m_i [\mathbf{r}_i - \mathbf{C}]\right)[\mathbf{d}]+ [\mathbf{d}]\left(\sum_{i=1}^n m_i [\mathbf{r}_i - \mathbf{C}]\right)

\left(\sum_{i=1}^n m_i\right) [\mathbf{d}]^2.

첫 번째 항은 질량중심을 기준으로 한 관성 모멘트 행렬

\mathbf{I_C}

이다. 두 번째와 세 번째 항은 질량중심

\mathbf{C}

의 정의에 따라 0이다. 마지막 항은 계의 총질량에

\mathbf{d}

로 구성된 비대칭 행렬

[\mathbf{d}]

의 제곱을 곱한 값이다.

결과적으로 평행축 정리는 다음과 같다.

:

\mathbf{I}_\mathbf{R} = \mathbf{I}_\mathbf{C} - M[\mathbf{d}]^2,

여기서

\mathbf{d}

는 질량중심

\mathbf{C}

에서 기준점

\mathbf{R}

로 향하는 벡터이다.

회전축이 질량중심을 지날 때 관성 모멘트는 최솟값을 가지며, 축이 질량중심으로부터 거리

h

만큼 떨어져 있을 경우, 그 축 주위의 관성 모멘트

I_h

는

:

I_h = I_\mathrm{G}+Mh^2

이 된다.^[38]

3. 2. 주축과 주관성 모멘트

물체의 고정된 좌표계에서 관성 텐서는 상수 실수 대칭 행렬이다. 실수 대칭 행렬은 회전 행렬

\mathbf{Q}

과 대각 행렬

\boldsymbol{\Lambda}

의 곱으로 고유값 분해될 수 있으며, 다음과 같이 표현된다.

\mathbf{I}_\mathbf{C}^B = \mathbf{Q}\boldsymbol{\Lambda}\mathbf{Q}^\mathsf{T},

여기서

\boldsymbol{\Lambda} = \begin{bmatrix}I_1 & 0 & 0 \\0 & I_2 & 0 \\0 & 0 & I_3\end{bmatrix}.

회전 행렬

\mathbf{Q}

의 열 벡터는 물체의 주축 방향을 정의하며, 상수

I_1

,

I_2

,

I_3

는 '''주 관성 모멘트'''라고 한다. 이 결과는 J. J. 실베스터 (1852)에 의해 처음으로 제시되었으며, 실베스터의 관성 법칙의 한 형태이다.^[29]^[30] 가장 큰 관성 모멘트를 갖는 주축을 때로는 '''장축''' 또는 '''형상축'''이라고 한다.

장난감 팽이는 회전하는 강체의 예이며, "팽이"라는 용어는 강체의 종류를 나타내는 이름에 사용된다. 모든 주 관성 모멘트가 서로 다를 때, 질량중심을 지나는 주축은 유일하게 결정되며, 이 강체를 '''비대칭 팽이'''라고 한다. 두 개의 주 관성 모멘트가 같으면, 강체를 '''대칭 팽이'''라고 하며, 두 개의 대응하는 주축에 대한 선택은 유일하지 않다. 세 개의 주 관성 모멘트가 모두 같으면, 강체를 '''구형 팽이'''라고 하며(반드시 구형일 필요는 없다), 임의의 축을 주축으로 간주할 수 있으므로, 임의의 축에 대한 관성 모멘트는 동일하다.

주축은 종종 물체의 대칭축에 정렬된다. 강체가 차수

m

의 대칭축을 가지고 있다면, 즉 주어진 축에 대해 회전에 대해 대칭적이라면, 그 축은 주축이다.

m > 2

일 때, 강체는 대칭 팽이이다. 강체가 서로 평행하거나 수직이 아닌 두 개 이상의 대칭축을 가지고 있다면, 예를 들어 정육면체 또는 다른 플라톤 입체와 같이 구형 팽이이다.

운동하는 차량은 종종 요, 피치, 롤 즉 세 개의 주축에 대한 회전에 대략적으로 해당하는 용어로 설명된다. 차량이 좌우 대칭이라면, 주축 중 하나는 횡축(피치축)에 정확히 대응한다.

이 수학적 현상의 실용적인 예로는 자동차의 일반적인 작업인 타이어 밸런싱이 있는데, 이는 기본적으로 자동차 바퀴의 질량 분포를 조정하여 관성의 주축이 차축과 정렬되도록 하여 바퀴가 흔들리지 않도록 하는 것을 의미한다.

회전하는 분자는 비대칭, 대칭 또는 구형 팽이로 분류되며, 회전 스펙트럼의 구조는 각 유형에 따라 다르다.

체좌표계에서 관성 모멘트 행렬은 체의 표면을 정의하는 2차 형태이며, 이는 푸앵소의 타원체라고 불린다.^[31] 질량 중심을 기준으로 주축에 정렬된 관성 행렬을

\boldsymbol{\Lambda}

라고 하면, 다음과 같은 표면

\mathbf{x}^\mathsf{T}\boldsymbol{\Lambda}\mathbf{x} = 1,

또는

I_1x^2 + I_2y^2 + I_3z^2 =1,

은 체 좌표계에서 타원체를 정의한다. 이 방정식을 다음 형태로 쓴다.

\left(\frac{x}{1/\sqrt{I_1}}\right)^2 + \left(\frac{y}{1/\sqrt{I_2}}\right)^2 + \left(\frac{z}{1/\sqrt{I_3}}\right)^2 = 1,

이 타원체의 반주축은 다음과 같이 주어진다.

a = \frac{1}{\sqrt{I_1}}, \quad b=\frac{1}{\sqrt{I_2}}, \quad c=\frac{1}{\sqrt{I_3}}.

이 타원체 위의 한 점

\mathbf{x}

를 크기와 방향으로 정의한다.

\mathbf{x} = \|\mathbf{x}\|\mathbf{n}

여기서

\mathbf{n}

은 단위 벡터이다. 그러면 위에 제시된 관성 행렬과

\mathbf{n}

방향의 축을 중심으로 한 스칼라 관성 모멘트

I_\mathbf{n}

사이의 관계는 다음과 같다.

\mathbf{x}^\mathsf{T}\boldsymbol{\Lambda}\mathbf{x} = \|\mathbf{x}\|^2\mathbf{n}^\mathsf{T}\boldsymbol{\Lambda}\mathbf{n} = \|\mathbf{x}\|^2 I_\mathbf{n} = 1.

따라서 관성 타원체 위의

\mathbf{n}

방향의 한 점

\mathbf{x}

의 크기는

\|\mathbf{x}\| = \frac{1}{\sqrt{I_\mathbf{n}}}.

이다.

관성 텐서 행렬은 실대칭행렬이므로, 적절한 직교좌표계를 선택하여 대각화할 수 있으며, 그때의 좌표축을 '''관성 주축'''이라 하고, 관성 모멘트를 '''주관성 모멘트'''라고 한다.^[37] 관성 주축 좌표계에서는 각운동량은 다음과 같이 간단하게 나타낼 수 있다.

:

\begin{pmatrix}L_1\\L_2\\L_3\end{pmatrix} = \begin{pmatrix}I_1&0&0\\0&I_2&0\\0&0&I_3\end{pmatrix} \begin{pmatrix}\omega_1\\ \omega_2\\ \omega_3\end{pmatrix}

3. 3. 회전 운동 에너지

물체가 축을 중심으로 자유롭게 회전할 때, 각운동량을 바꾸려면 토크가 필요하다. 주어진 각가속도(각속도의 변화율)를 만드는 데 필요한 토크는 물체의 관성 모멘트에 비례한다. 관성 모멘트는 SI 단위로 킬로그램 제곱미터(kg·m²)로 나타낼 수 있다.^[2]

관성 모멘트는 회전 운동에서 질량이 직선 운동에서 하는 역할과 같다. 두 가지 모두 물체의 운동 변화에 얼마나 저항하는지를 나타낸다. 관성 모멘트는 회전축을 기준으로 질량이 어떻게 분포하는지에 따라 달라지며, 축에 따라 그 값이 달라진다. 점 질량의 경우, 어떤 축에 대한 관성 모멘트는

mr^2

로 주어지는데, 여기서

r

은 점과 축 사이의 거리이고,

m

은 질량이다.

레온하르트 오일러는 1765년 그의 저서 ''Theoria motus corporum solidorum seu rigidorum''에서 "관성 모멘트"("momentum inertiae" in 라틴어)라는 용어를 처음 사용했다.^[2]^[3]

관성 모멘트는 또한 계의 총 각운동량을 주축 주위의 각속도로 나눈 값으로 정의된다.^[8]^[9]

:

I = \frac{L}{\omega}.

만약 계의 각운동량이 일정하다면, 관성 모멘트가 작아질수록 각속도는 커져야 한다. 이는 회전하는 피겨 스케이터가 팔을 안으로 당기거나 다이버가 다이빙 중에 몸을 웅크리는 자세를 취해 더 빨리 회전할 때 나타난다.^[8]^[9]^[10]^[11]^[12]^[13]^[14]

물체의 모양이 변하지 않으면 관성 모멘트는 뉴턴 운동 법칙에서 물체에 작용하는 토크와 주축 주위의 각가속도의 비율로 나타난다.

:

\tau = I \alpha.

일반적으로 질량을 가진 물체가 주어지면 특정 회전축에 따라 의존하는 유효 반지름을 정의할 수 있으며, 이 반지름을 사용하면 축 주위의 관성 모멘트는 다음과 같다.

:

I = m k^2,

여기서는 축 주위의 회전반경이다.

강체가 고정 평면과 평행하게 움직이도록 제한되는 경우, 회전은 이 평면과 평행한 축

\mathbf{\hat{k}}

주위에서 발생한다. 이 경우, 질량의 관성 모멘트는 ''극 관성 모멘트''이다. 극 관성 모멘트의 정의는 강체 입자계의 평면 운동에 대한 운동량, 운동 에너지, 뉴턴의 법칙을 고려하여 얻을 수 있다.^[15]^[22]^[25]^[26]

n

개의 입자

P_i, i = 1, \dots, n

의 계가 강체로 조립된 경우, 운동량은 기준점

\mathbf{R}

에 대한 상대 위치와 절대 속도

\mathbf{v}_i

의 관점에서 쓸 수 있다.

:

\begin{align}\Delta\mathbf{r}_i &= \mathbf{r}_i - \mathbf{R}, \\\mathbf{v}_i &= \boldsymbol{\omega} \times \left(\mathbf{r}_i - \mathbf{R}\right) + \mathbf{V}= \boldsymbol{\omega} \times \Delta\mathbf{r}_i + \mathbf{V},\end{align}

여기서

\boldsymbol{\omega}

는 계의 각속도이고

\mathbf{V}

는

\mathbf{R}

의 속도이다.

평면 운동의 경우 각속도 벡터는 운동 평면에 수직인 단위 벡터

\mathbf{k}

를 따라 향한다. 기준점

\mathbf{R}

에서 점

\mathbf{r}_i

까지의 단위 벡터

\mathbf{e}_i

와 단위 벡터

\mathbf{\hat{t}}_i = \mathbf{\hat{k}} \times \mathbf{\hat{e}}_i

를 도입하면,

:

\begin{align}\mathbf{\hat{e}}_i &= \frac{\Delta\mathbf{r}_i}{\Delta r_i},\quad\mathbf{\hat{k}}  = \frac{\boldsymbol{\omega}}{\omega},\quad\mathbf{\hat{t}}_i  = \mathbf{\hat{k}} \times \mathbf{\hat{e}}_i, \\\mathbf{v}_i &= \boldsymbol{\omega} \times \Delta\mathbf{r}_i + \mathbf{V}= \omega\mathbf{\hat{k}} \times \Delta r_i\mathbf{\hat{e}}_i + \mathbf{V}= \omega\, \Delta r_i\mathbf{\hat{t}}_i + \mathbf{V}\end{align}

이는 평면에서 움직이는 입자의 강체계에 대한 상대 위치 벡터와 속도 벡터를 정의한다.

강체 입자계의 평면 운동에 대한 각운동량 벡터는 다음과 같이 주어진다.^[15]^[22]

:

\begin{align}\mathbf{L} &= \sum_{i=1}^n m_i \Delta\mathbf{r}_i \times \mathbf{v}_i \\&= \sum_{i=1}^n m_i \,\Delta r_i\mathbf{\hat{e}}_i \times \left(\omega\, \Delta r_i\mathbf{\hat{t}}_i + \mathbf{V}\right) \\&= \left(\sum_{i=1}^n m_i \,\Delta r_i^2\right)\omega \mathbf{\hat{k}} +\left(\sum_{i=1}^n m_i\,\Delta r_i\mathbf{\hat{e}}_i\right) \times \mathbf{V}.\end{align}

질량 중심

\mathbf{C}

을 기준점으로 사용하면

:

\begin{align}\Delta r_i \mathbf{\hat{e}}_i &= \mathbf{r}_i - \mathbf{C}, \\\sum_{i=1}^n m_i\,\Delta r_i \mathbf{\hat{e}}_i &= 0,\end{align}

이고, 질량 중심에 대한 관성 모멘트

I_\mathbf{C}

를 다음과 같이 정의한다.

:

I_\mathbf{C} = \sum_{i} m_i\,\Delta r_i^2,

그러면 각운동량에 대한 방정식은 다음과 같이 간소화된다.^[23]

:

\mathbf{L} = I_\mathbf{C} \omega \mathbf{\hat{k}}.

강체계의 운동에 수직이고 질량 중심을 지나는 축에 대한 관성 모멘트

I_\mathbf{C}

는 ''극관성 모멘트''이다.

평면상에서 운동하는 강체 입자계의 운동 에너지는 다음과 같이 주어진다.^[15]^[22]

:

\begin{align}E_\text{K}&= \frac{1}{2} \sum_{i=1}^n m_i \mathbf{v}_i \cdot \mathbf{v}_i, \\&= \frac{1}{2} \sum_{i=1}^n m_i\left(\omega \,\Delta r_i\mathbf{\hat{t}}_i + \mathbf{V}\right) \cdot\left(\omega \,\Delta r_i\mathbf{\hat{t}}_i + \mathbf{V}\right), \\&= \frac{1}{2}\omega^2 \left(\sum_{i=1}^n m_i\, \Delta r_i^2 \mathbf{\hat{t}}_i \cdot \mathbf{\hat{t}}_i\right) +\omega\mathbf{V} \cdot \left(\sum_{i=1}^n m_i \,\Delta r_i\mathbf{\hat{t}}_i\right) +\frac{1}{2}\left(\sum_{i=1}^n m_i\right) \mathbf{V} \cdot \mathbf{V}.\end{align}

기준점을 계의 질량 중심

\mathbf{C}

로 하면 두 번째 항은 0이 되고, 관성 모멘트

I_\mathbf{C}

를 도입하면 운동 에너지는 다음과 같이 주어진다.^[23]

:

E_\text{K} = \frac{1}{2} I_\mathbf{C} \omega^2 + \frac{1}{2} M\mathbf{V} \cdot \mathbf{V}.

관성 모멘트

I_\mathbf{C}

는 물체의 극관성모멘트이다.

n개의 입자 Pi, i = 1, ..., n으로 구성된 강체계에 대한 뉴턴의 법칙은 기준점 R에서의 합력과 토크로 표현할 수 있으며,^[15]^[22]

:

\begin{align}\mathbf{F} &= \sum_{i=1}^n m_i\mathbf{A}_i, \\\boldsymbol\tau &= \sum_{i=1}^n \Delta\mathbf{r}_i \times m_i\mathbf{A}_i,\end{align}

여기서 ri는 각 입자의 궤적을 나타낸다.

강체의 운동학은 기준 입자의 위치 R과 가속도 A뿐만 아니라 입자계의 각속도 벡터 ω와 각가속도 벡터 α에 대한 입자 Pi의 가속도 공식을 제공한다.

:

\mathbf{A}_i =\boldsymbol\alpha \times \Delta\mathbf{r}_i + \boldsymbol{\omega} \times \boldsymbol{\omega} \times \Delta\mathbf{r}_i + \mathbf{A}.

평면 운동으로 제한된 계의 경우, 각속도와 각가속도 벡터는 운동면에 수직인 k 방향으로 향하며, 이는 가속도 방정식을 단순화한다. 이 경우, 기준점 R에서 점 ri까지의 단위 벡터 ei와 단위 벡터 ti = k × ei를 도입하여 가속도 벡터를 단순화할 수 있다.

:

\begin{align}\mathbf{A}_i&= \alpha\mathbf{\hat{k}} \times \Delta r_i\mathbf{\hat{e}}_i - \omega\mathbf{\hat{k}} \times \omega\mathbf{\hat{k}} \times \Delta r_i\mathbf{\hat{e}}_i + \mathbf{A} \\&= \alpha \Delta r_i\mathbf{\hat{t}}_i - \omega^2 \Delta r_i\mathbf{\hat{e}}_i + \mathbf{A}.\end{align}

이것은 계에 대한 합력 토크를 생성한다.

:

\begin{align}\boldsymbol{\tau} &= \sum_{i=1}^n m_i\,\Delta r_i\mathbf{\hat{e}}_i \times \left(\alpha\Delta r_i\mathbf{\hat{t}}_i - \omega^2\Delta r_i\mathbf{\hat{e}}_i + \mathbf{A}\right) \\&= \left(\sum_{i=1}^n m_i\,\Delta r_i^2\right)\alpha \mathbf{\hat{k}} + \left(\sum_{i=1}^n m_i\,\Delta r_i\mathbf{\hat{e}}_i\right) \times\mathbf{A},\end{align}

여기서 ei × ei = 0이고, ei × ti = k는 모든 입자 Pi에 대해 평면에 수직인 단위 벡터이다.

질량중심 C를 기준점으로 사용하고 질량중심에 대한 관성 모멘트 IC를 정의하면, 합력 토크에 대한 방정식은 다음과 같이 단순화된다.^[23]

:

\boldsymbol{\tau} = I_\mathbf{C}\alpha\mathbf{\hat{k}}.

4. 계산 예시

물체의 축에 대한 관성 모멘트는 물체의 모든 입자에 대해 $mr^2$ 을 합산하여 계산하며, 여기서 $r$ 은 지정된 축에 대한 수직 거리이다. 확장된 물체의 운동 연구에서 관성 모멘트가 어떻게 발생하는지 확인하려면 강체 점 질량 조립체를 고려하는 것이 편리하다.^[21]

$N$ 개의 질량 $m_i$ 가 회전축의 가장 가까운 점인 피벗 지점 $P$ 에서 $r_i$ 거리에 있는 조립체의 운동 에너지는 개별 질량의 운동 에너지의 합으로 주어진다.^[22]^[23]

: $E_\text{K} =\sum_{i=1}^N \frac{1}{2}\,m_i \mathbf{v}_i \cdot \mathbf{v}_i =\sum_{i=1}^N \frac{1}{2}\,m_i \left(\omega r_i\right)^2 =\frac12\, \omega^2 \sum_{i=1}^N m_i r_i^2.$

따라서 물체의 관성 모멘트는 각 $mr^2$ 항의 합으로 표현된다.

: $I_P = \sum_{i=1}^N m_i r_i^2.$

즉, 관성 모멘트는 회전축 주위의 입자의 질량과 분포를 결합하는 물리적 특성이다. 동일한 물체의 서로 다른 축을 중심으로 한 회전은 서로 다른 관성 모멘트를 생성한다.

지정된 축을 중심으로 회전하는 연속체의 관성 모멘트는 무한히 많은 점 입자를 제외하고는 동일한 방식으로 계산된다. 따라서 합산의 한계가 제거되고 합은 다음과 같이 작성된다.

: $I_P = \sum_i m_i r_i^2$

이는 적분을 이용하여 다음과 같이 표현할 수 있다.

: $I_P = \iiint_{Q} \rho(x, y, z) \left\|\mathbf{r}\right\|^2 dV$

여기서 $\rho$ 는 각 점 $(x, y, z)$ 에서 질량 밀도를 나타내는 함수이고, $\mathbf{r}$ 은 회전축에 수직이고 회전축의 한 점에서 고체의 점 $(x, y, z)$ 까지 연장되는 벡터이며, 적분은 물체 $Q$ 의 부피 $V$ 에 대해 평가된다. 평면 표면의 관성 모멘트는 질량 밀도가 면적 질량 밀도로 대체되고 적분이 면적에 대해 평가되는 것과 유사하다.

'''면적의 2차 모멘트에 대한 주석''': 평면에서 움직이는 물체의 관성 모멘트와 면적의 2차 모멘트는 종종 혼동된다. 단면의 모양을 가진 물체의 관성 모멘트는 단면에 수직인 $z$ 축에 대한 이 면적의 2차 모멘트이며, 밀도에 의해 가중치가 부여된다. 이것은 또한 ''면적의 극 모멘트''라고도 하며, $x$ 축과 $y$ 축에 대한 2차 모멘트의 합이다.^[24] 보의 응력은 하중에 따라 $x$ 축 또는 $y$ 축 주위의 단면적의 2차 모멘트를 사용하여 계산된다.

몇 가지 간단한 형태의 물체에 대한 관성 모멘트 계산 예시는 다음과 같다.

가는 막대
직사각형 판
꽉 찬 구
원판
링 모양 원판

4. 1. 가는 막대

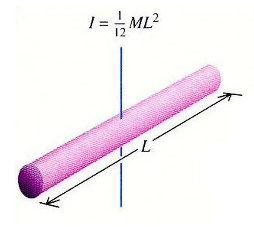
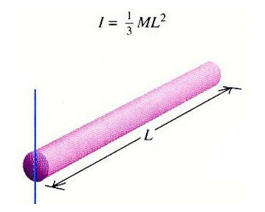
막대의 질량을 거리의 관계식으로 나타내면 다음과 같다.

:

M=\rho L

이 질량소를 이용해 관성모멘트를 구하기 위해

dm

에 대입하여 계산하면 축을 기준으로 회전하는 막대의 한 쪽 부분의 관성모멘트가 구해진다.

하지만 우리가 구하려는 값은 막대의 중심축으로 회전하는 관성모멘트이므로 2를 곱하여 계산하면

:

\begin{align}I&=2\int_0^\frac L2r^2\,dm\\&=2\rho\int_0^\frac L2r^2\,dr\\&=\frac1{12}\rho L^3\\&=\frac1{12}ML^2\end{align}

:

\therefore I=\frac1{12}ML^2

같은 방법으로 막대 끝을 축으로 회전하는 관성 모멘트를 구하면 다음과 같다.

:

M=\rho L

:

dm=\rho dr

:

\begin{align}I&=\int_0^Lr^2\,dm\\&=\rho\int_0^Lr^2\,dr\\&=\frac13\rho L^3\\&=\frac13ML^2\end{align}

:

\therefore I=\frac13ML^2

얇은 막대 끝에 장착된 얇은 원반으로 구성된 '''복합 진자'''의 관성 모멘트는 막대와 원반의 질량 중심에 대한 관성 모멘트 계산으로 시작된다.^[23]

일정한 단면적 $s$ , 밀도 $\rho$ , 길이 $\ell$ 을 갖는 '''얇은 막대'''의 질량 중심을 통과하는 수직 축에 대한 관성 모멘트는 적분을 통해 결정된다.^[23] $x$ 축을 막대와 정렬하고 원점을 막대 중심의 질량 중심에 위치시키면,

I_{C, \text{rod}} = \iiint_Q \rho\,x^2 \, dV =\int_{-\frac{\ell}{2}}^\frac{\ell}{2} \rho\,x^2 s\, dx =\left. \rho s\frac{x^3}{3}\right|_{-\frac{\ell}{2}}^\frac{\ell}{2} =\frac{\rho s}{3} \left(\frac{\ell^3}{8} + \frac{\ell^3}{8}\right) =\frac{m\ell^2}{12},

여기서

m = \rho s \ell

은 막대의 질량이다.

무게를 무시할 수 있는 길이

L

의 막대 양 끝에 질량

m

과

M

의 물체가 붙어 있다고 생각하자. 막대의 적절한 위치에 회전 중심이 되는 점을 정하고, 거기서 양 끝까지의 팔 길이를 각각

a

와

L-a

라고 하자. 이때, 중심에 대한 관성 모멘트

I

는,

:

I = m a^2 + M (L-a)^2 = (m+M)\left(a-\frac{M}{m+M}L\right)^2+\frac{mM}{m+M}L^2

로 계산된다. 이 식에서 알 수 있듯이, 관성 모멘트는 중심(회전축)의 위치에 따라 그 값이 달라진다. 중심으로 계의 중심을 취했을 때, 관성 모멘트는 최소가 된다. 즉, 가장 회전하기 쉽다.

4. 2. 직사각형 판

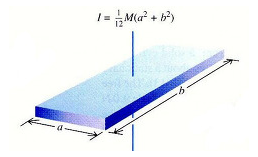
가로와 세로가 각각 a, b인 직사각형 판의 넓이는 ab이므로, 이 직사각형 물체의 질량과 질량소는 다음과 같이 나타낼 수 있다.

:M|M^영어 = ρ|로^영어ab

:dm|dm^영어 = ρ|로^영어dadb

이때 직사각형 위의 임의의 원자 위치를 a와 b를 이용하여 나타내면 다음과 같다.

:r|r^영어² = a² + b²

위에서 구한 값들을 각 항에 대입하면 다음과 같은 식이 유도된다.

:I|I^영어 = ∫r|r^영어²dm|dm^영어 = ∫(a² + b²)ρ|로^영어dadb

적분 범위가 가로 a와 세로 b 두 개이므로 중적분을 하여 계산한다. 이때 위의 식은 직사각형 판의 1/4에 해당하는 부분이므로, 전체 식에 4를 곱하여 직사각형 중심을 지나는 축으로 회전하는 물체의 관성 모멘트를 구한다.

:I|I^영어 = 4ρ|로^영어∫₀^{b|b^영어/2}∫₀^{a|a^영어/2}(a² + b²)dadb

:= 4ρ|로^영어∫₀^{b|b^영어/2}[1/3a³ + ab²]₀^{a|a^영어/2}db

:= 4ρ|로^영어∫₀^{b|b^영어/2}[1/3a³/8 + a/2b²]db

:= 4ρ|로^영어[1/24a³b + a/6b³]₀^{b|b^영어/2}

:= 4ρ|로^영어[1/192a³b + 1/48ab³]

:= ρ|로^영어ab/48 * 4(a² + b²)

:= M|M^영어/12(a² + b²)

따라서,

:I|I^영어 = M|M^영어/12(a² + b²)

4. 3. 꽉 찬 구

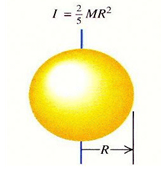
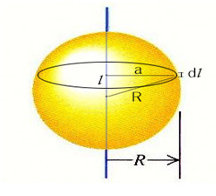
이 디스크의 질량소와 구의 질량은 다음과 같다.

:

M=\frac{4}{3}\pi\rho R^3

:

dm=\pi a^2\rho\,dl=\rho\pi\left(R^2-l^2\right)\,dl

관성 모멘트를 구하면 다음과 같다.

:

\begin{align}di&=\frac{1}{2}\pi\left(R^2-l^2\right)\rho\left(R^2-l^2\right)\,dl\\&=\frac{1}{2}\pi\rho\left(R^2-l^2\right)^2\,dl\\&=\frac{1}{2}\pi\rho\left(R^4-2R^2l^2+l^4\right)\,dl\\\end{align}

:

\begin{align}I&=\int \,di\\&=\int_{-R}^R\frac{1}{2}\pi\rho\left(R^4-2R^2l^2+l^4\right)\,dl\\&=\pi\rho\int_0^R\left(R^4-2R^2l^2+l^4\right)\, dl\\&=\pi\rho\left[R^4l-\frac{2}{3}R^2l^3+\frac{1}{5}l^5\right]_0^R\\&=\pi\rho\left(R^5-\frac{2}{3}R^5+\frac{1}{5}R^5\right)\\&=\frac{8}{15}\pi\rho R^5\\&=\frac{4}{3}\pi R^3\rho\,\frac{2}{5}R^2\\&=\frac{2}{5}MR^2\end{align}

:

\therefore I=\frac{2}{5}MR^2

4. 4. 원판

밀도가 일정하고 반지름이 , 전체 질량이 인 균일한 원판의 중심축 주위 관성 모멘트는 다음과 같이 계산된다.

먼저, 중심에서 반지름 이고 폭이 인 고리의 질량 를 고려하면,

이다. 여기서 는 원판의 밀도이다.

이 고리의 관성 모멘트 는

이다.

따라서 전체 원판의 관성 모멘트는 이 고리들의 관성 모멘트를 0부터 까지 적분하여 구할 수 있다.

최종적으로, 원판의 관성 모멘트는

이다.

4. 5. 링 모양 원판

바깥 반지름 , 안쪽 반지름 , 전체 질량 인 링 모양 원판의 경우, 앞서 구한 를 이용하여

이 된다.

5. 관련 물리량

관성 모멘트는 주어진 축을 중심으로 회전하는 물체의 운동 변화에 저항하는 정도를 나타내는 물리량이다. 예를 들어 질량은 같지만 반지름이 다른 두 원판 A와 B를 생각해보자. A의 반지름이 더 크고 질량 분포가 균일하다면, 같은 각속도로 회전할 때 A의 바깥쪽은 B보다 더 빠르게 움직인다. 따라서 A를 돌리는 것이 B를 돌리는 것보다 어렵다. 이 경우 A의 관성 모멘트는 B보다 크다.

텐서 형태에는 두 종류가 있다. 도르래처럼 회전축이 고정된 물체는 스칼라 형태를 사용하여 물리량 사이의 관계를 간단하게 기술할 수 있다. 그러나 회전축이 변하는 자이로스코프, 팽이, 인공위성 운동과 같이 복잡한 경우에는 각운동량 벡터와 각속도 벡터가 평행하지 않아 스칼라 형태로 관계를 기술하기 어렵기 때문에 텐서 형태를 사용한다.

기계공학자들은 단면 이차 모멘트와 구별하기 위해 관성 모멘트를 '''질량 관성 모멘트'''(mass moment of inertia^영어)라고 부르기도 한다. 이 둘을 구별하는 가장 쉬운 방법은 단위를 비교하는 것이다. 또한, 관성 모멘트는 물체가 비틀림에 저항하는 능력을 나타내는 극관성모멘트와 혼동하지 않도록 주의해야 한다.

물체가 축 주위로 자유롭게 회전할 수 있을 때, 토크를 가해야 각운동량을 변화시킬 수 있다. 주어진 각가속도(각속도의 변화율)를 발생시키는 데 필요한 토크의 양은 물체의 관성 모멘트에 비례한다. 관성 모멘트는 SI 단위계에서 킬로그램 제곱미터(kg·m²)로, 영국 단위계 또는 미국 단위계에서 파운드-피트-제곱초(lbf·ft·s²)로 나타낼 수 있다.

관성 모멘트는 회전 운동역학에서 질량(관성)이 직선 운동역학에서 하는 역할과 같다. 둘 다 물체의 운동 변화에 대한 저항을 나타낸다. 관성 모멘트는 회전축 주위에 질량이 어떻게 분포되어 있는지에 따라 달라지며, 선택한 축에 따라 값이 달라진다. 점 질량의 경우, 어떤 축에 대한 관성 모멘트는 $mr^2$ 로 주어지는데, 여기서 $r$ 은 점과 축 사이의 거리이고, $m$ 은 질량이다. 넓이가 있는 강체의 경우, 관성 모멘트는 회전축으로부터의 거리의 제곱에 질량의 미소량을 곱한 값들의 합이다. 규칙적인 모양과 균일한 밀도를 가진 넓이가 있는 물체의 경우, 이 합산은 때때로 물체의 치수, 모양 및 총 질량에 따라 달라지는 간단한 식을 생성한다.

1673년, 크리스티안 하위헌스는 복합진자라고 알려진, 회전축에 매달린 물체의 진동 연구에서 이 매개변수를 도입했다.^[2] "관성 모멘트"("momentum inertiae" in 라틴어)라는 용어는 레온하르트 오일러가 1765년 그의 저서 ''Theoria motus corporum solidorum seu rigidorum''에서 처음 사용했으며,^[2]^[3] 오일러의 제2 운동 법칙에 포함된다.

복합진자의 고유 진동수는 중력이 진자의 질량에 가하는 토크와 관성 모멘트에 의해 정의된 가속도에 대한 저항의 비율로부터 얻어진다. 이 고유 진동수를 단일 질점으로 구성된 단진자의 고유 진동수와 비교하면 넓이가 있는 물체의 관성 모멘트에 대한 수학적 공식을 얻을 수 있다.^[4]^[5]

관성 모멘트는 각운동량, 운동 에너지, 그리고 뉴턴 운동 법칙에서 물체의 모양과 질량을 결합하는 물리적 매개변수로 나타난다. 평면 운동에서는 관성 모멘트를 정의하는 단일 스칼라 값이 있지만, 공간 운동의 경우 동일한 계산으로 관성 모멘트의 3 × 3 행렬인 관성 행렬 또는 관성 텐서가 생성된다.^[6]^[7]

회전하는 플라이휠의 관성 모멘트는 기계에서 가해지는 토크의 변화에 대한 저항으로 사용되어 회전 출력을 부드럽게 한다. 비행기의 세로축, 수평축 및 수직축에 대한 관성 모멘트는 날개, 승강타 및 방향타의 조종면에 작용하는 조종력이 롤, 피치 및 요 운동에 어떻게 영향을 미치는지 결정한다.

관성 모멘트 ()는 또한 계의 총 각운동량 ()을 주축 주위의 각속도 ()로 나눈 값으로 정의된다.^[8]^[9] 즉,

$I = \frac{L}{\omega}.$

계의 각운동량이 일정하다면 관성 모멘트가 작아질수록 각속도는 증가해야 한다. 이는 회전하는 피겨 스케이터가 뻗은 팔을 안으로 당기거나 다이버가 다이빙 중에 몸을 몸을 웅크리는 자세로 만들어 더 빨리 회전할 때 발생한다.^[8]^[9]^[10]^[11]^[12]^[13]^[14]

물체의 모양이 변하지 않으면 관성 모멘트는 뉴턴 운동 법칙에 물체에 작용하는 토크 ()와 주축 주위의 각가속도 ()의 비율로 나타난다. 즉,

$\tau = I \alpha.$

단진자의 경우 이 정의는 진자의 질량 ()과 회전축으로부터의 거리 ()에 대한 관성 모멘트 ()에 대한 공식을 다음과 같이 제공한다.

$I = mr^2.$

따라서 진자의 관성 모멘트는 물체의 질량 ()과 회전축까지의 거리 ()로 정의된 기하학적 형태 모두에 따라 달라진다.

복합진자는 회전축 주위를 강체로 회전하는 연속적인 형태의 입자들의 집합체로 이루어진 물체이다. 복합진자의 관성 모멘트는 그것을 구성하는 각 입자의 관성 모멘트의 합이다.^[15]^[16]^[17] 복합진자의 고유 진동수 ()는 관성 모멘트 ()에 따라 달라지며,

$\omega_\text{n} = \sqrt{\frac{mgr}{I_P}},$

로 나타낼 수 있다. 여기서 은 물체의 질량, 는 국지적 중력 가속도, 은 회전축에서 물체의 질량 중심까지의 거리이다. 작은 각변위에 대한 이 진동 주파수를 측정하면 물체의 관성 모멘트를 효과적으로 측정할 수 있다.^[22]

따라서 물체의 관성 모멘트를 결정하려면, 편리한 회전축 에 물체를 매달아 원하는 관성 모멘트 방향에 수직인 평면에서 자유롭게 진동하도록 한 다음, 고유 진동수 또는 진동 주기 ()를 측정하여 다음 식을 얻는다.

$I_P = \frac{mgr}{\omega_\text{n}^2} = \frac{mgrt^2}{4\pi^2},$

여기서 는 진동 주기(지속 시간)이며, 일반적으로 여러 주기의 평균값을 사용한다.

5. 1. 회전 반지름

관성 모멘트()는 물체의 질량()에 비례하므로, 다음과 같이 쓸 수 있다.

:

I = M\kappa^2

여기서 는 길이의 차원을 가지며, 회전 반지름이라고 한다.^[38]

5. 2. 플라이휠 효과

관성 모멘트와 같은 의미를 갖는 물리량으로, 지름 를 이용하여 정의되는 플라이휠 효과 가 있다.

중력 단위계에서는, 강체의 중량 [kgf|킬로그램포스^한국어]와 지름 [m]을 이용한 양 을 플라이휠 효과라고 하며, 단위는 [kgf m²]이다. 관성 모멘트 와는 차원이 다르며, 로 환산한다 (는 중력 가속도)^[40]^[41]^[42]。
국제단위계에서는, 강체의 질량 [kg|킬로그램^한국어]와 지름 [m]을 이용한 양 을 플라이휠 효과라고 하며, 단위는 [kg m²]이다. 관성 모멘트 와 로 환산한다^[43]^[44]^[45]^[46]^[47]。

6. 응용

물체가 축 주위로 자유롭게 회전할 수 있을 때, 토크를 가해야 각운동량을 변화시킬 수 있다. 주어진 각가속도(즉, 각속도의 변화율)를 발생시키는 데 필요한 토크의 양은 물체의 관성 모멘트에 비례한다. 관성 모멘트는 SI 단위계에서 킬로그램 제곱미터(kg·m²)로, 영국 단위계 또는 미국 단위계에서 파운드-피트-제곱초(lbf·ft·s²)로 나타낼 수 있다.

관성 모멘트는 회전 운동역학에서 질량(관성)이 직선 운동역학에서 하는 역할과 같으며, 물체의 운동 변화에 대한 저항을 나타낸다. 관성 모멘트는 회전축 주위에 질량이 어떻게 분포되어 있는지에 따라 달라지며, 선택한 축에 따라 값이 달라진다.

공학 분야에서 회전축에 관성 모멘트가 큰 회전체를 부착한 장치를 플라이휠(flywheel, 회전체)이라고 한다. 이것은 회전 속도의 급격한 변화를 억제하거나, 회전에 의한 에너지를 저장하는 목적으로 사용된다. 회전하는 플라이휠의 관성 모멘트는 기계에서 가해지는 토크의 변화에 대한 저항으로 사용되어 회전 출력을 부드럽게 한다. 비행기의 세로축, 수평축 및 수직축에 대한 관성 모멘트는 날개, 승강타 및 방향타의 조종면에 작용하는 조종력이 롤, 피치 및 요 운동에 어떻게 영향을 미치는지 결정한다.

7. 추가 정보

물체가 축 주위로 자유롭게 회전할 때, 토크를 가해야 각운동량을 변화시킬 수 있다. 주어진 각가속도(즉, 각속도의 변화율)를 발생시키는 데 필요한 토크의 양은 물체의 관성 모멘트에 비례한다. 관성 모멘트는 SI 단위계에서 킬로그램 제곱미터(kg·m²)로, 영국 단위계 또는 미국 단위계에서 파운드-피트-제곱초(lbf·ft·s²)로 나타낼 수 있다.

관성 모멘트는 회전 운동역학에서 질량(관성)이 직선 운동역학에서 하는 역할과 같다. 둘 다 물체의 운동 변화에 대한 저항을 나타낸다. 관성 모멘트는 회전축 주위에 질량이 어떻게 분포되어 있는지에 따라 달라지며, 선택한 축에 따라 값이 달라진다. 점 질량의 경우, 어떤 축에 대한 관성 모멘트는 `mr^2`로 주어지는데, 여기서 `r`은 점과 축 사이의 거리이고, `m`은 질량이다. 넓이가 있는 강체의 경우, 관성 모멘트는 회전축으로부터의 거리의 제곱에 질량의 미소량을 곱한 값들의 합이다. 규칙적인 모양과 균일한 밀도를 가진 넓이가 있는 물체의 경우, 이 합산은 때때로 물체의 치수, 모양 및 총 질량에 따라 달라지는 간단한 식을 생성한다.

1673년, 크리스티안 하위헌스는 복합진자라고 알려진, 회전축에 매달린 물체의 진동 연구에서 이 매개변수를 도입했다. "관성 모멘트"("momentum inertiae" in 라틴어)라는 용어는 레온하르트 오일러가 1765년 그의 저서 ''Theoria motus corporum solidorum seu rigidorum''에서 처음 사용했으며,^[3] 오일러의 제2 운동 법칙에 포함된다.

복합진자의 고유 진동수는 중력이 진자의 질량에 가하는 토크와 관성 모멘트에 의해 정의된 가속도에 대한 저항의 비율로부터 얻어진다. 이 고유 진동수를 단일 질점으로 구성된 단진자의 고유 진동수와 비교하면 넓이가 있는 물체의 관성 모멘트에 대한 수학적 공식을 얻을 수 있다.^[4]^[5]

관성 모멘트는 각운동량, 운동 에너지, 그리고 뉴턴 운동 법칙에서 물체의 모양과 질량을 결합하는 물리적 매개변수로 나타난다. 관성 모멘트가 평면 운동과 공간 운동에서 나타나는 방식에는 흥미로운 차이가 있다. 평면 운동에서는 관성 모멘트를 정의하는 단일 스칼라 값이 있지만, 공간 운동의 경우 동일한 계산으로 관성 모멘트의 3 × 3 행렬인 관성 행렬 또는 관성 텐서가 생성된다.^[6]^[7]

회전하는 플라이휠의 관성 모멘트는 기계에서 가해지는 토크의 변화에 대한 저항으로 사용되어 회전 출력을 부드럽게 한다. 비행기의 세로축, 수평축 및 수직축에 대한 관성 모멘트는 날개, 승강타 및 방향타의 조종면에 작용하는 조종력이 롤, 피치 및 요 운동에 어떻게 영향을 미치는지 결정한다.

참조

_[1] 서적 A Dictionary of Mechanical Engineering http://www.oxfordref[...] Oxford University Press 2019
_[2] 서적 The Science of Mechanics https://archive.org/[...] 2014-11-21
_[3] 서적 Theoria motus corporum solidorum seu rigidorum: Ex primis nostrae cognitionis principiis stabilita et ad omnes motus, qui in huiusmodi corpora cadere possunt, accommodata [The theory of motion of solid or rigid bodies: established from first principles of our knowledge and appropriate for all motions which can occur in such bodies.] https://archive.org/[...] A. F. Röse 1765
_[4] 서적 Classical dynamics of particles & systems https://archive.org/[...] Thomson
_[5] 서적 Mechanics Addison-Wesley
_[6] 서적 Fundamentals of Applied Dynamics Springer
_[7] 서적 Dynamics, Theory and Applications McGraw-Hill
_[8] 서적 Introduction to Understandable Physics: Volume I - Mechanics https://books.google[...] AuthorHouse 2010
_[9] 서적 Honors Physics Essentials https://books.google[...] Silly Beagle Productions 2011
_[10] 웹사이트 Spinning Ice Skater http://demonstration[...] Mathematica, Inc. 2014-09-30
_[11] 웹사이트 Figure Skating Spins http://www.bsharp.or[...] 2014-09-30
_[12] 서적 New Understanding Physics for Advanced Level https://books.google[...] Nelson Thomas 2000
_[13] 서적 Conservation Laws https://archive.org/[...] Light and Matter 2003
_[14] 서적 Physics for Scientists and Engineers, Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics https://books.google[...] Macmillan 1999
_[15] 서적 Kinematics and Dynamics of Planar Machinery Prentice Hall 1979-06
_[16] 서적 Fundamentals of physics Wiley
_[17] 서적 Vibrations and waves CRC Press
_[18] 웹사이트 Trifilar Pendulum for MOI https://www.happrese[...] 2016
_[19] 간행물 The experimental determination of the moments of inertia of airplanes by a simplified compound-pendulum method https://digital.libr[...] 1948
_[20] 서적 Statics and Strengths of Materials Prentice Hall 2011
_[21] 문서 In that situation this moment of inertia only describes how a torque applied along that axis causes a rotation about that axis. But, torques not aligned along a principal axis will also cause rotations about other axes.
_[22] 서적 Theory of Machines and Mechanisms Oxford University Press
_[23] 서적 Vector mechanics for engineers: Dynamics McGraw-Hill
_[24] 서적 Analysis and Design of Elastic Beams: Computational Methods https://books.google[...] John Wiley
_[25] 서적 Classical Mechanics Addison-Wesley
_[26] 서적 Mechanics https://archive.org/[...] Pergamon Press
_[27] 서적 Robot Analysis: The mechanics of serial and parallel manipulators John-Wiley
_[28] 웹사이트 Physically Based Modeling - Rigid Body Simulation http://graphics.pixa[...]
_[29] 학술지 A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares http://www.maths.ed.[...] 2008-06-27
_[30] 서적 Undergraduate algebra Oxford University Press
_[31] 서적 Mechanics of Robotics Manipulation https://books.google[...] MIT Press 2014-11-21
_[32] 서적 式(5-2)
_[33] 서적
_[34] 서적
_[35] 서적
_[36] 논문
_[37] 논문
_[38] 논문
_[39] 논문
_[40] 서적 小型モーターのしくみ電波新聞社
_[41] 서적 機械力学入門理工学社
_[42] 서적 小型モータとその使い方日刊工業新聞社
_[43] 서적 JEC-2130　同期機電気書院
_[44] 서적 JIS B 0119 水車及びポンプ水車用語日本規格協会
_[45] 서적 電気設備用語辞典オーム社
_[46] 서적 モータ技術用語辞典日刊工業新聞社
_[47] 서적 電気用語辞典コロナ社
_[48] 서적 Theoria motus corporum solidorum seu rigidorum: ex primis nostrae cognitionis principiis stabilita et ad omnes motus, qui in huiusmodi corpora cadere possunt, accommodata http://www.17century[...] 2012-02-18

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com